Ontdek de Magie van Delen en Gehelen

Stel je voor: een heerlijke taart, versgebakken en klaar om te delen. Hoe verdeel je die eerlijk over al je vrienden? Dat is waar het begrip 'delen van een geheel' om de hoek komt kijken. Van het snijden van een pizza tot het berekenen van kortingen in de winkel, het begrijpen van hoe delen zich verhouden tot het geheel is een essentiële vaardigheid die ons dagelijks leven doordringt.
Het concept 'sommen deel van het geheel' draait om de relatie tussen een kleiner deel en het grotere geheel waartoe het behoort. Of het nu gaat om breuken, percentages, verhoudingen of decimalen, de kern is hetzelfde: we proberen te begrijpen hoeveel een bepaald deel bijdraagt aan het totaal. Deze ogenschijnlijk eenvoudige relatie heeft verreikende gevolgen, van het begrijpen van statistieken tot het koken van de perfecte maaltijd.
De geschiedenis van het rekenen met delen van een geheel gaat ver terug. Al in de oudheid worstelden beschavingen met het verdelen van land, goederen en tijd. De Egyptenaren gebruikten bijvoorbeeld breuken om land op te meten langs de Nijl, terwijl de Babyloniërs een geavanceerd systeem van zestigdelige breuken ontwikkelden dat nog steeds de basis vormt van onze tijdmeting. Het belang van deze berekeningen is door de eeuwen heen alleen maar toegenomen.
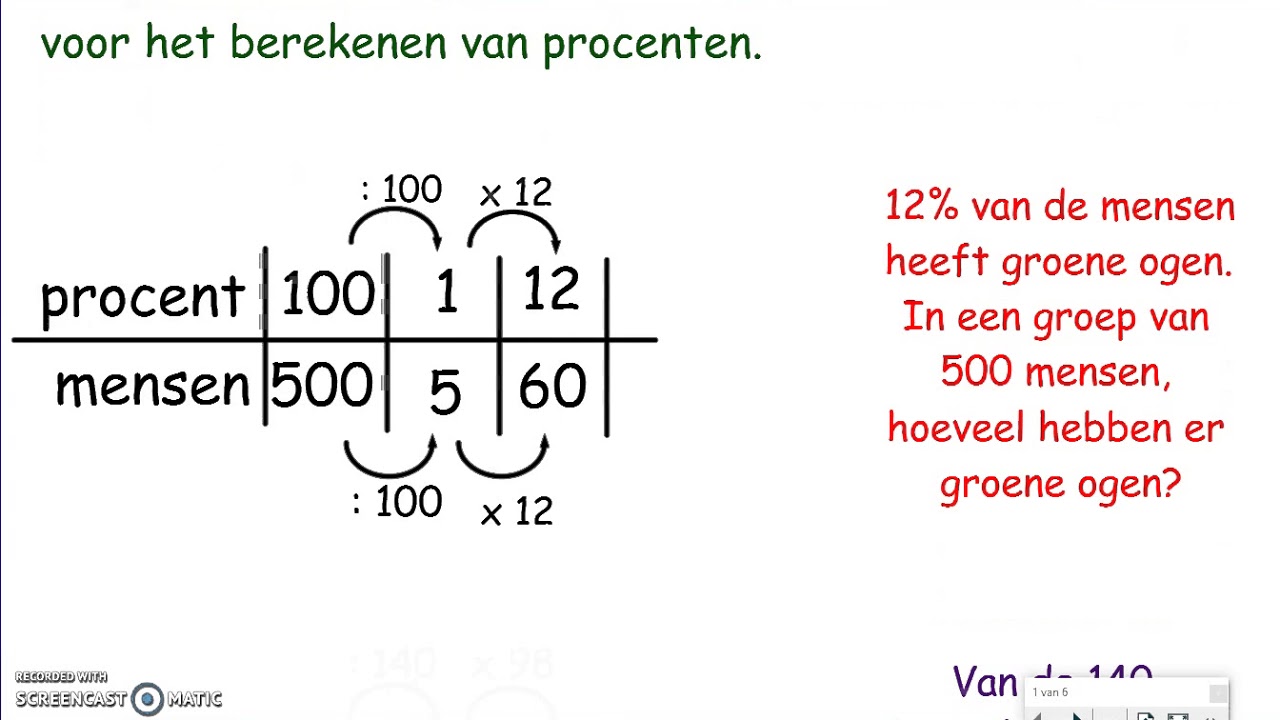
Een veelvoorkomend probleem bij het werken met delen van een geheel is het vinden van het juiste formaat om de relatie uit te drukken. Soms is een percentage het meest geschikt, terwijl in andere gevallen een breuk of decimaal getal duidelijker is. Het kiezen van de juiste representatie is cruciaal voor een accurate interpretatie en effectieve communicatie.
Een ander belangrijk aspect is het beheersen van de verschillende bewerkingen met delen van een geheel. Optellen, aftrekken, vermenigvuldigen en delen van breuken, percentages en decimalen vereist specifieke regels en technieken. Het begrijpen van deze regels is essentieel voor het oplossen van complexe problemen in diverse contexten, van financiën tot wetenschap.
Een eenvoudig voorbeeld: als je 3/4 van een pizza hebt opgegeten, hoeveel is er dan nog over? Het antwoord is 1/4, omdat het geheel (de hele pizza) wordt voorgesteld door 4/4, en 4/4 - 3/4 = 1/4.
Voordelen van het beheersen van sommen met delen van het geheel zijn talrijk. Ten eerste verbetert het je financiële geletterdheid. Je kunt budgetteren, kortingen berekenen en investeringsbeslissingen nemen. Ten tweede vergroot het je probleemoplossend vermogen. Je kunt complexe problemen opsplitsen in kleinere, beheersbare delen. Ten derde versterkt het je analytisch vermogen. Je kunt data interpreteren, trends identificeren en weloverwogen conclusies trekken.
Een actieplan om je vaardigheden te verbeteren kan bestaan uit het oefenen met online rekentools, het bestuderen van voorbeelden en het toepassen van de concepten in dagelijkse situaties.
Voor- en Nadelen van Werken met Delen van een Geheel
Veelgestelde vragen:
1. Wat is een breuk? Antwoord: Een breuk drukt een deel van een geheel uit.
2. Hoe bereken je een percentage? Antwoord: Deel het deel door het geheel en vermenigvuldig met 100.
3. Wat is een verhouding? Antwoord: Een vergelijking van twee of meer hoeveelheden.
4. Hoe zet je een breuk om in een decimaal getal? Antwoord: Deel de teller door de noemer.
5. Hoe tel je breuken op? Antwoord: Zorg voor een gelijke noemer en tel de tellers op.
6. Wat is het verschil tussen een deel en een geheel? Antwoord: Een deel is een fractie van het geheel.
7. Hoe bereken je een korting? Antwoord: Vermenigvuldig het percentage korting met de oorspronkelijke prijs.
8. Hoe gebruik je delen van een geheel bij het koken? Antwoord: Bij het aanpassen van recepten voor meer of minder personen.
Tips en trucs: Visualiseer de relatie tussen deel en geheel met behulp van diagrammen of afbeeldingen. Oefen regelmatig met verschillende soorten opgaven. Zoek hulp online of bij een docent als je vastloopt.
Kortom, het begrijpen van 'sommen deel van het geheel' is een fundamentele vaardigheid met een rijke geschiedenis en talloze toepassingen in ons dagelijks leven. Of het nu gaat om het verdelen van een taart, het berekenen van kortingen of het interpreteren van statistieken, het beheersen van deze concepten stelt ons in staat om de wereld om ons heen beter te begrijpen en effectiever te navigeren. Door te oefenen en de verschillende representaties en bewerkingen te beheersen, kunnen we onze analytische vaardigheden versterken en weloverwogen beslissingen nemen in diverse contexten. Investeer in je kennis van delen en gehelen en ontdek de kracht van deze essentiële wiskundige principes.
Hindoe jongensnamen met de letter p een betekenisvolle keuze
Doorbraak met humor de kunst van komische rollen
De magie van ragdoll cat fotos