Découvrir les fonctions en 3ème : Un atout pour les maths

Comment représenter une relation entre deux grandeurs ? C'est une question fondamentale en mathématiques, et la réponse se trouve souvent dans l'étude des fonctions. En 3ème, la découverte des fonctions marque une étape importante dans votre apprentissage des mathématiques. Cet article vous guidera à travers les bases de ce concept essentiel.

Les fonctions en mathématiques, introduites en 3ème, permettent de modéliser des situations de la vie courante. Imaginez que vous achetez des pommes au marché. Le prix total que vous payez dépend du nombre de pommes que vous achetez. Cette relation entre le nombre de pommes et le prix total est un exemple de fonction.

L'histoire des fonctions remonte à l'Antiquité, avec des contributions de mathématiciens comme Leibniz et Euler. L'idée de relier des variables entre elles est apparue progressivement, permettant de décrire et d'analyser des phénomènes divers, des trajectoires des planètes aux variations de température.

Maîtriser les fonctions en 3ème est crucial pour poursuivre sereinement vos études de mathématiques. Ce concept est la base de nombreux autres sujets abordés au lycée et au-delà, comme les équations, les inéquations et la géométrie analytique. Comprendre les fonctions, c'est acquérir une clé pour décrypter le monde qui nous entoure.

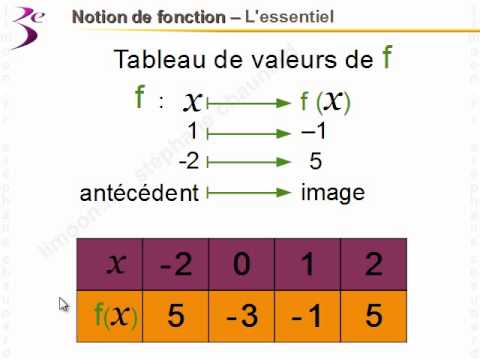
Un des principaux problèmes rencontrés par les élèves face aux fonctions est la difficulté à visualiser la relation entre les variables. Il est important de se familiariser avec les différents modes de représentation : tableaux de valeurs, graphiques et expressions algébriques. La pratique régulière est la clé pour surmonter cette difficulté.

Une fonction est une relation qui, à chaque valeur de la variable x (appelée antécédent), associe une unique valeur de la variable y (appelée image). On note souvent une fonction f(x), par exemple, f(x) = 2x + 1. Si x = 3, alors f(3) = 2*3 + 1 = 7. 7 est l'image de 3 par la fonction f.

Exemples : Le périmètre d'un carré est une fonction de la longueur de son côté. La distance parcourue par une voiture à vitesse constante est une fonction du temps. L'aire d'un cercle est une fonction de son rayon.

Avantages des fonctions : 1. Modélisation : elles permettent de représenter des situations réelles. 2. Prédiction : elles permettent d'anticiper des résultats. 3. Analyse : elles permettent d'étudier les variations et les propriétés des relations entre grandeurs.

Plan d'action : 1. Revoir le cours et les définitions. 2. S'entraîner avec des exercices variés. 3. Demander de l'aide au professeur si besoin.

Avantages et Inconvénients des Fonctions en 3ème

Avantages	Inconvénients
Facilite la compréhension des relations entre grandeurs	Peut être abstrait au début
Permet de modéliser des situations concrètes	Nécessite de la pratique pour la maîtrise
Outil essentiel pour les mathématiques futures

FAQ : 1. Qu'est-ce qu'une fonction ? 2. Comment représenter une fonction ? 3. Qu'est-ce qu'un antécédent ? 4. Qu'est-ce qu'une image ? 5. Comment calculer l'image d'un nombre par une fonction ? 6. À quoi servent les fonctions en mathématiques ? 7. Comment tracer le graphique d'une fonction ? 8. Comment interpréter le graphique d'une fonction ?

Conseils : N'hésitez pas à utiliser des couleurs et des graphiques pour visualiser les fonctions. Refaites les exercices corrigés en classe pour vous assurer de bien comprendre.

En conclusion, les fonctions en 3ème sont un outil puissant pour comprendre et modéliser les relations entre les grandeurs. Elles constituent une base solide pour vos futures études mathématiques et vous ouvrent les portes à une meilleure compréhension du monde qui vous entoure. Maîtriser ce concept est un atout précieux, alors n'hésitez pas à pratiquer et à approfondir vos connaissances sur les fonctions ! N'oubliez pas que la pratique régulière et la visualisation sont les clés de la réussite. Continuez à explorer le monde fascinant des fonctions et vous découvrirez leurs nombreuses applications et leur utilité au quotidien.

Duree de validite dun dbs tout savoir
Decryptage des mes 07 e que mes mystere ou realite
Dechainer larsenal datomic heart guide ultime des armes