Quadratische Geheimnisse Die Basis entschlüsseln

Hast du dich jemals gefragt, wie man die Seitenlänge eines Quadrats bestimmt, wenn man nur seine Fläche kennt? Die Berechnung der Basis eines Quadrats, auch bekannt als Seitenlänge, ist ein grundlegendes Konzept in der Geometrie und findet Anwendung in vielen Bereichen des Lebens, vom Bauwesen bis zur Kunst.

Die Bestimmung der Seitenlänge eines Quadrats, wenn die Fläche gegeben ist, mag zunächst kompliziert erscheinen, ist aber eigentlich ganz einfach. Es erfordert lediglich das Verständnis des Konzepts der Quadratwurzel. Die Fläche eines Quadrats ist definiert als die Seitenlänge multipliziert mit sich selbst. Umgekehrt ist die Seitenlänge die Quadratwurzel aus der Fläche.

Die Berechnung der Quadratseite – ein mathematisches Rätsel, das uns seit Jahrhunderten begleitet. Von den alten Ägyptern, die Quadrate zur Landvermessung nutzten, bis zu modernen Architekten, die sie in ihren Bauplänen verwenden – das Quadrat und seine Eigenschaften sind allgegenwärtig. Das Verständnis seiner Berechnung ist der Schlüssel zum Verständnis vieler geometrischer Konzepte.

Die Bedeutung der Seitenlängenberechnung liegt nicht nur in der Mathematik selbst. Sie ist ein Werkzeug, das uns hilft, die Welt um uns herum zu verstehen und zu gestalten. Stell dir vor, du möchtest einen quadratischen Garten anlegen und kennst nur die gewünschte Fläche. Die Berechnung der Seitenlänge hilft dir, die benötigten Materialien und den Platzbedarf genau zu bestimmen.

In diesem Artikel werden wir die verschiedenen Methoden zur Berechnung der Basis eines Quadrats genauer untersuchen, von einfachen Beispielen bis hin zu komplexeren Szenarien. Du wirst lernen, wie du die Quadratwurzel ziehst und welche praktischen Anwendungen sich daraus ergeben. Bereit, die Geheimnisse des Quadrats zu lüften?

Die Geschichte der Quadratwurzelberechnung reicht weit zurück. Bereits die Babylonier entwickelten vor über 4000 Jahren Methoden zur Approximation von Quadratwurzeln. Die Bedeutung der Berechnung der Quadratseite liegt in ihrer fundamentalen Rolle in der Geometrie und Mathematik. Ein Hauptproblem kann die Schwierigkeit sein, die Quadratwurzel von Zahlen ohne Taschenrechner zu berechnen.

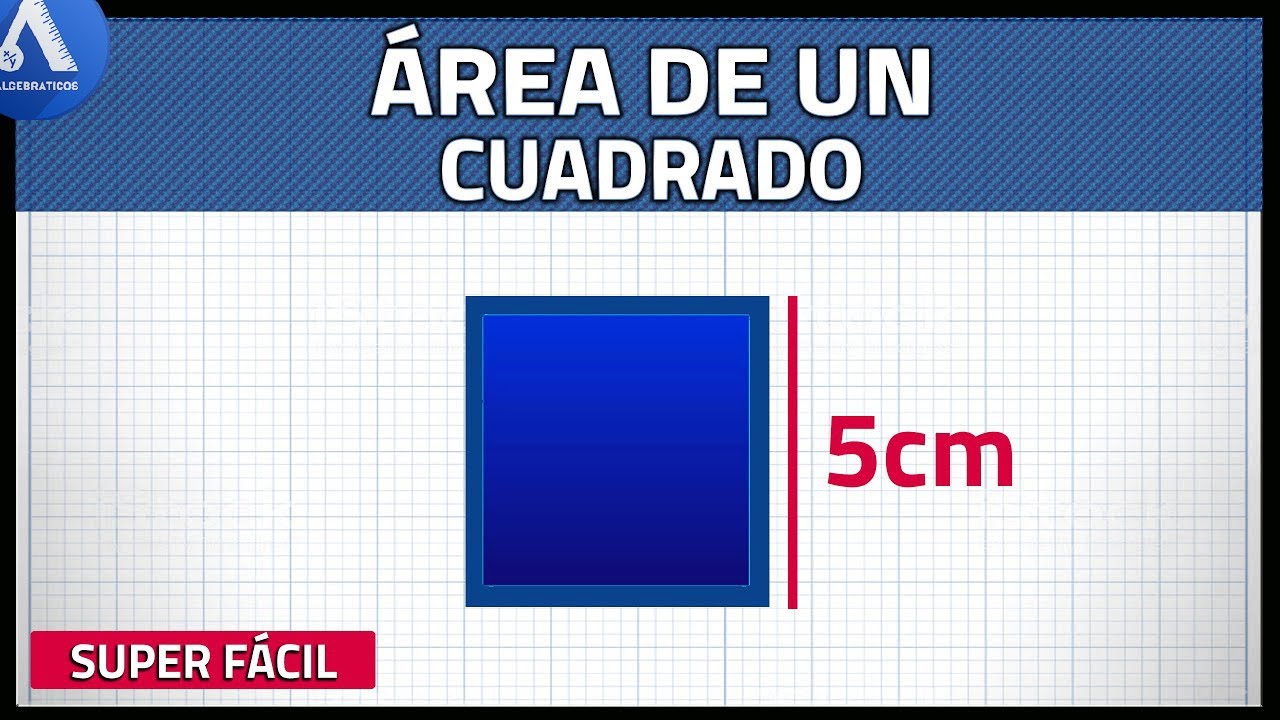
Die Basis (Seitenlänge) eines Quadrats ist die Strecke, die zwei seiner benachbarten Eckpunkte verbindet. Um die Basis zu berechnen, wenn die Fläche gegeben ist, zieht man die Quadratwurzel aus der Fläche. Beispiel: Fläche = 25 cm², Basis = √25 cm² = 5 cm.

Vorteile der Basisberechnung: 1. Ermöglicht die Berechnung des Umfangs. 2. Hilft bei der Konstruktion von Quadraten mit vorgegebener Fläche. 3. Fundamentales Wissen für viele geometrische Berechnungen.

Aktionsplan: 1. Fläche bestimmen. 2. Quadratwurzel aus der Fläche ziehen. 3. Ergebnis als Basis notieren.

Checkliste: Fläche bekannt? Taschenrechner vorhanden? Einheit der Basis angeben?

Schritt-für-Schritt-Anleitung: 1. Schreibe die Fläche auf. 2. Benutze einen Taschenrechner oder eine Tabelle, um die Quadratwurzel zu ziehen. 3. Notiere die Basis mit der entsprechenden Einheit.

Häufig gestellte Fragen: 1. Was ist die Basis eines Quadrats? 2. Wie berechnet man die Basis, wenn die Fläche gegeben ist? 3. Was ist die Quadratwurzel? 4. Wozu braucht man die Basisberechnung im Alltag? 5. Wie berechnet man die Fläche eines Quadrats? 6. Was ist der Unterschied zwischen Basis und Umfang? 7. Gibt es Online-Rechner für die Basisberechnung? 8. Wie berechnet man die Basis ohne Taschenrechner?

Tipps und Tricks: Nutze einen Taschenrechner für schnelles Rechnen. Merke dir die Quadratzahlen für einfache Berechnungen.

Zusammenfassend lässt sich sagen, dass die Berechnung der Basis eines Quadrats ein grundlegendes Konzept in der Geometrie ist, das weitreichende Anwendungen hat. Von der Planung eines Gartens bis hin zu komplexen architektonischen Berechnungen ist das Verständnis der Beziehung zwischen Fläche und Seitenlänge unerlässlich. Die Beherrschung dieser Fähigkeit eröffnet Türen zu einem tieferen Verständnis der Mathematik und ihrer Anwendung in der realen Welt. Beginne noch heute damit, die Geheimnisse des Quadrats zu erforschen und entdecke die faszinierende Welt der Geometrie. Durch die Kenntnis der Basisberechnung eröffnen sich zahlreiche Möglichkeiten, mathematische Probleme zu lösen und die Welt um uns herum besser zu verstehen. Nutze die hier vorgestellten Tipps und Tricks, um deine Fähigkeiten zu verbessern und die Berechnung der Basis eines Quadrats zu meistern.

Coco chanel parfum die essenz einer legende
Das mysterium des unbekannten textes entschlusseln
Mh im text bedeutung und nutzung in der online kommunikation