Grenzkostenfunktion verstehen und anwenden

Wie viel kostet die Produktion einer zusätzlichen Einheit? Diese Frage beantwortet die Grenzkostenfunktion. Sie ist ein zentrales Konzept in der Mikroökonomie und hilft Unternehmen, optimale Produktionsmengen zu bestimmen.

Die Grenzkostenfunktion leitet sich von der Kostenfunktion ab und beschreibt die Veränderung der Gesamtkosten bei der Herstellung einer zusätzlichen Einheit. Sie liefert wertvolle Informationen für die Preisgestaltung und Produktionsentscheidungen.

In diesem Artikel erklären wir Ihnen einfach und verständlich, wie Sie die Grenzkostenfunktion berechnen und interpretieren können. Wir zeigen Ihnen, wie dieses Werkzeug Ihnen helfen kann, die Profitabilität Ihres Unternehmens zu steigern.

Die Grenzkostenberechnung ist essenziell für jedes Unternehmen, das seine Kosten optimieren und seinen Gewinn maximieren möchte. Verständnis der Grenzkosten ermöglicht fundierte Entscheidungen über Produktionsmengen und Preise.

Von der Theorie zur Praxis: Wir bieten Ihnen konkrete Beispiele und praktische Tipps, um die Grenzkostenfunktion effektiv in Ihrem Unternehmen anzuwenden.

Die Grenzkostenfunktion hat ihre Wurzeln in der neoklassischen Wirtschaftstheorie. Sie spielt eine wichtige Rolle in der Kosten-Nutzen-Analyse und hilft Unternehmen, die effizienteste Produktionsmenge zu identifizieren.

Ein zentrales Problem im Zusammenhang mit der Grenzkostenfunktion ist die genaue Bestimmung der Kostenfunktion. In der Praxis ist es oft schwierig, alle Kostenfaktoren zu berücksichtigen.

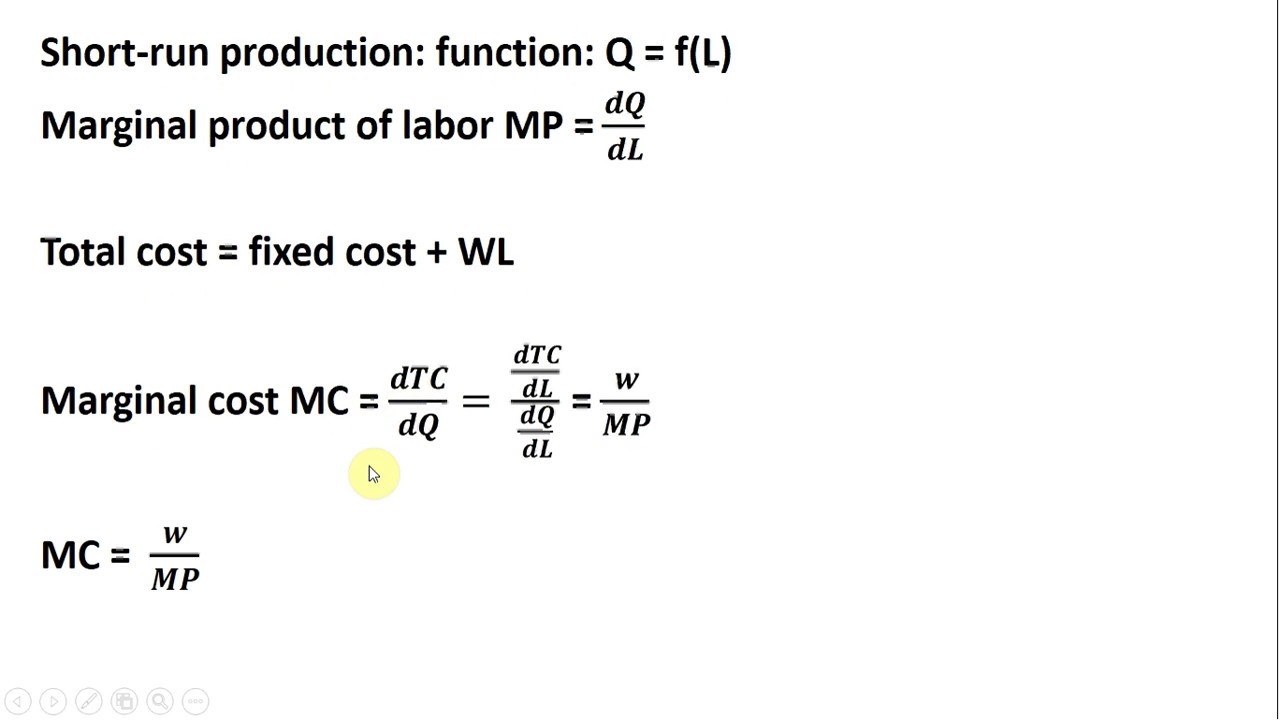
Die Grenzkostenfunktion wird mathematisch als die erste Ableitung der Kostenfunktion definiert. Sie gibt die Steigung der Kostenfunktion an einem bestimmten Punkt an.

Beispiel: Wenn die Kostenfunktion K(x) = 2x² + 5x + 10 ist, dann ist die Grenzkostenfunktion K'(x) = 4x + 5. Wenn x = 10 ist, dann sind die Grenzkosten K'(10) = 45.

Vorteile der Grenzkostenfunktion:

1. Optimale Produktionsmenge: Die Grenzkostenfunktion hilft Unternehmen, die Produktionsmenge zu bestimmen, bei der der Gewinn maximiert wird.

2. Preisgestaltung: Die Grenzkosten können als Grundlage für die Preisgestaltung dienen, um sicherzustellen, dass die Kosten gedeckt sind und ein Gewinn erzielt wird.

3. Kostenkontrolle: Die Grenzkostenfunktion hilft, die Kostenentwicklung zu analysieren und Ineffizienzen zu identifizieren.

Aktionsplan: Analysieren Sie Ihre Kostenfunktion, leiten Sie die Grenzkostenfunktion ab, und verwenden Sie diese Informationen, um Ihre Produktionsentscheidungen zu optimieren.

Vor- und Nachteile der Grenzkostenfunktion

Vorteile	Nachteile
Optimierung der Produktionsmenge	Komplexität der Berechnung bei komplexen Kostenfunktionen
Fundierte Preisgestaltung	Vereinfachende Annahmen in der Theorie
Verbesserte Kostenkontrolle	Schwierigkeit der genauen Kostenerfassung in der Praxis

Häufig gestellte Fragen:

1. Was ist die Grenzkostenfunktion? - Die Grenzkostenfunktion beschreibt die Kostenänderung bei der Produktion einer zusätzlichen Einheit.

2. Wie berechnet man die Grenzkostenfunktion? - Durch Ableitung der Kostenfunktion.

3. Wozu dient die Grenzkostenfunktion? - Zur Optimierung der Produktionsmenge und Preisgestaltung.

4. Was ist der Zusammenhang zwischen Grenzkosten und Kostenfunktion? - Die Grenzkostenfunktion ist die Ableitung der Kostenfunktion.

5. Wie hilft die Grenzkostenfunktion bei der Gewinnmaximierung? - Indem sie die optimale Produktionsmenge aufzeigt.

6. Was sind die Grenzen der Grenzkostenfunktion? - Die Komplexität der Berechnung und vereinfachende Annahmen.

7. Wie kann ich die Grenzkostenfunktion in meinem Unternehmen anwenden? - Durch Analyse der Kosten und Ableitung der Grenzkostenfunktion.

8. Wo finde ich weitere Informationen zur Grenzkostenfunktion? - In Lehrbüchern der Mikroökonomie.

Tipps und Tricks: Verwenden Sie Software zur Berechnung der Grenzkostenfunktion. Berücksichtigen Sie alle relevanten Kostenfaktoren. Analysieren Sie die Grenzkosten regelmäßig, um auf Marktveränderungen zu reagieren.

Die Grenzkostenfunktion ist ein unverzichtbares Werkzeug für jedes Unternehmen, das seine Kosten optimieren und seinen Gewinn maximieren möchte. Sie ermöglicht fundierte Entscheidungen über Produktionsmengen und Preise, indem sie die Kostenänderung bei der Herstellung einer zusätzlichen Einheit beschreibt. Die Berechnung der Grenzkostenfunktion mag zwar zunächst komplex erscheinen, aber die Vorteile, die sie bietet, überwiegen bei weitem. Durch die Anwendung der Grenzkostenfunktion können Unternehmen ihre Effizienz steigern und ihre Wettbewerbsfähigkeit verbessern. Nutzen Sie dieses wertvolle Instrument, um Ihr Unternehmen erfolgreich zu führen. Investieren Sie Zeit in das Verständnis und die Anwendung der Grenzkostenfunktion – es lohnt sich!

Strom grundpreis verstehen und optimieren
Astrologie im cafe bremerhaven dein kosmos und du
Kulinarische entdeckungen genussvolles essen zum mitnehmen in marbella